Types of Angles – Acute, Right, Obtuse, Straight, Reflex, and Complete Angles
During the studying of the geometry chapter in the classroom, we always hear some words from the teacher ‘Measure The Angle or Find out the angle’. We start looking for some protractors to measure the angle between the arms by placing them on the vertex points.
In this blog, we will get to know or learn about the basics of an angle i.e. elements connected with an angle, and the different types of angles we use in Mathematics.
What Are Angles?
When two rays or lines intersect with each other at a common point, an angle is created. Angles are measured in degrees and the important concept or backbone of the geometry chapter. In the field of engineering and architecture as well, it is impossible to take out the best measurements without using angles. The concept of angle can be seen in our daily life as well, from writing on paper to sitting on a chair.

Important Parts of An Angle
1. Vertex – A common meeting point where two lines or rays meet.
2. Arms – The arms are the two straight line segments generating from a vertex.
According to the above image, the common meeting point O is called Vertex while OB and OA are the two arms.
Note – The angle can be measured in both directions i.e. anti-clockwise direction or clockwise direction by taking one arm as initial side OB concerning another arm as terminal side OA.
Types of Angles in Geometry
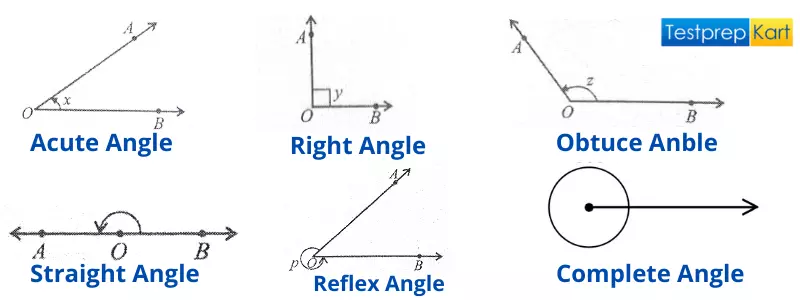
While talking about the types of angles, we mainly remember six types of angles in mathematics which are commonly used in the geometry chapter as per rotation factor. The six angles are
1. Acute Angle
2. Right Angle
3. Obtuse Angle
4. Straight Angle
5. Reflex Angle
6. Complete Angle
The complete explanation of the above angles is given below with figures for your better understanding –
1. Acute Angle – An angle is said to be an ‘acute angle’ when the angle lies between 0° and 90° in simple words, an angle that is less than 90° is called an acute angle.

Here, ∠AOB = x, 0° < x < 90°
2. Right Angle – An angle is said to be a 'right angle' only when it measures exactly 90°. It is formed only when two intersecting lines are perpendicular to each other.
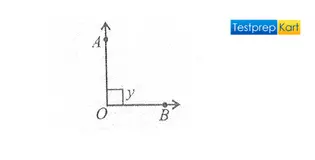
Here, ∠AOB = y, y = 90°
3. Obtuse Angle – An angle is said to be an 'obtuse angle' when the angle between two lines lies between 90 and 180 in simple words, we can say any angle which ranges from 90° to 180° or a mirror image of an acute angle.
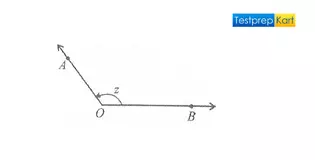
Here, ∠AOB = z, 90° < z < 180°
4. Straight Angle – An angle is said to be a 'straight angle' only when it is measured exactly 180° i.e. a normal straight line.
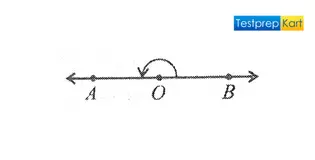
Here, ∠AOB = 180°
5. Reflex Angle – An angle which is said to be a 'reflex angle' only when it is greater than 180° and less than 360° or in other words, an angle that lies or ranges between 180° and 360°.
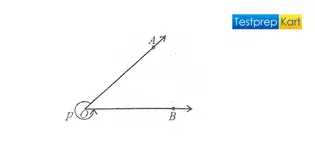
Here, Reflex ∠AOB = 360° – ∠AOB = p, 180° < p < 360°
6. Complete Angle – An angle is said to be a 'complete angle' or 360° when both the arms make a complete rotation from the initial position i.e. overlapping each other.
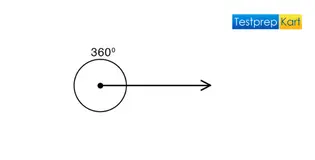
Here, a complete circle is formed which is equal to 360°
Summary Table of Angles
| Angle Name |
Description |
| Acute Angle |
0° < X > 90° |
| Right Angle |
X = 90° |
| Obtuse Angle |
90° < X > 180° |
| Straight Angle |
X = 180° |
| Reflex Angle |
180° < X> 360° |
| Complete Angle |
X = 360° |
Let 'X' be any angle
Some more information about Special Types of Angles
1. Adjacent Angles – Two angles are said to be adjacent angles, if
- They have the same vertex
- They have a common arm and
- Non-common arms are on either side of the common arm.
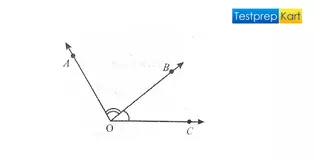
∠AOB and ∠BOC are adjacent angles
Note 1 – If a ray stands on a line, the sum of two adjacent angles so formed is 180°
Note 2 – If the sum of two adjacent angles is 180°, then the non-common arms of the angles are in a straight line.
2. Complementary and Supplementary Angles – If the sum of two angles is 90°, then they are 'complementary angles' while if the sum of two angles is 180°, then they are 'supplementary angles'.
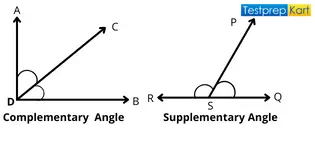
Here, ∠ADC + ∠BDC = 90° and ∠PSQ + ∠PSR = 180°
3. Linear Pair – If the sum of two adjacent angles is 180°, then they are said to form a 'linear pair'.
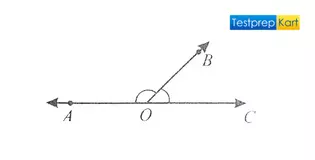
Here, ∠AOB + ∠COB = 180°
Some Regular Used angles with the concept of transversal line
Transversal line – A straight line intersecting two or more straight lines in distinct points is known as a 'transversal line'
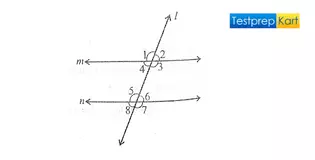
In the above figure, the line l is a transversal line that intersects two lines m and n, and forms different angles such as ∠ 1, ∠ 2, ∠ 4, ∠ 3, ∠ 6, ∠ 5, ∠ 7, and ∠8.
Exterior Angles – Exterior angles are the angles lying outside the region between the two lines, which are intersected by a transversal. According to the above figure, angles ∠ 1, ∠ 2, ∠ 7, and ∠8 are exterior angles.
Interior Angles – Interior angles are angles lying inside the region between the two lines, which are intersected by a transversal. According to the above figure, angles ∠ 4, ∠ 3, ∠ 6, ∠ and 5 are interior angles.
Corresponding Angles – These are pairs of angles lying on the same side of the transversal, both of which either lie above two lines or below the two intersected by a transversal. Angles ∠1 & ∠5, ∠2 & ∠6, ∠3 & ∠7, ∠4 & ∠8 are corresponding angles.
Alternate exterior Angles – These are pairs of angles lying in the region between the two lines and on the opposite sides of the transversal but one below the transversal and the other above the transversal. Here, ∠4 & ∠6 and ∠3 & ∠5 are alternate exterior angles.
Vertically Opposite Angles – If two lines AB and CD intersect each other at point O, then four angles are formed. Here, ∠1 & ∠3, ∠4 & ∠2, ∠6 & ∠8, ∠5 & ∠7 are vertically opposite angles.


Post a Comment