Cbse Class 11th Vector Addition – Analytical Method Details & Preparations Downloads

Vector addition is a fundamental mathematical operation that combines two or more vectors to produce a new vector, known as the resultant vector. Vectors are quantities that have both magnitude (size) and direction, and they are commonly represented as arrows in a coordinate system.

What is Vector Addition?

The process of vector addition involves combining the individual components of vectors to determine the components of the resultant vector. The addition of vectors can be visualised geometrically using the head-to-tail or parallelogram methods, and it can also be performed algebraically by adding the corresponding components of the vectors.

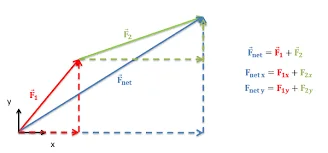
Geometric Representation:

• Head-to-Tail Method:

  • Place the tail of the second vector at the head of the first vector.

  • The resultant vector is drawn from the tail of the first vector to the head of the second vector.

• Parallelogram Method:

  • Draw the vectors as adjacent sides of a parallelogram.

  • The resultant vector is the diagonal of the parallelogram, starting from the common point of the vectors.

Algebraic Representation:

If you have two vectors A=⟨ax,Ay⟩ and B=⟨Bx,By⟩, their sum A+B is given by:

A+B=⟨Ax+Bx,Ay+By⟩

For three-dimensional space, you would extend this to three components.

Properties of Vector Addition:

Commutative Property: Vector addition is commutative, meaning the order in which you add the vectors does not affect the result.

A+B=B+A.

Associative Property: Vector addition is associative, meaning that when adding more than two vectors, the result is the same regardless of how the vectors are grouped.

Zero Vector: Adding a zero vector to any vector does not change the vector. IfA+0=A.

Download Physics notes 

Parallelogram Law of Vector Addition :

The Parallelogram Law of Vector Addition is a geometric method used to add two vectors. It states that the sum of two vectors is represented by the diagonal of the parallelogram formed by the vectors. This law is based on the principle that vectors can be treated as directed line segments.

Statement of the Parallelogram Law:

For two vectors

A and B, the vector sum

A+B is represented by the diagonal of the parallelogram formed by the vectors. Mathematically, this can be expressed as:

A+B=Diagonal of the Parallelogram

Method of Using the Parallelogram Law:

Draw the Vectors:

Start by drawing the vectors A and B as arrows with their tails at the same point.

Complete the Parallelogram:

Draw lines parallel to A and B to form a parallelogram. The vectors A and B are now adjacent sides of the parallelogram.

Example:

Let A=⟨3,2⟩ and B=⟨−1,4⟩. Using the Parallelogram Law:

• Draw vectors A and B with their tails at the same point.

• Form a parallelogram with A and B as adjacent sides.

• The diagonal of the parallelogram represents

• A+B.

• Measure the length of the diagonal to find the magnitude.

• Determine the direction of the resultant vector.

Triangular Law of Vector Addition :

Statement of the Triangular Law:

For two vector

A and B, the vector sum A+B is represented by the third side of the triangle formed by the vectors. Mathematically, this can be expressed as:

A+B=Third Side of the Triangle

Method of Using the Triangular Law:

Draw the Vectors:

• Start by drawing the vectors

• A and B as arrows with their tails at the same point.

Complete the Triangle:

• Draw a line from the head of

• A to the head of B to complete the triangle. The vectors

• A and B are now two sides of the triangle.

Identify the Third Side:

• The vector sum A+B is represented by the third side of the triangle, which starts from the tail of A and ends at the head of B.

Why is Vector Addition Important?

Vector addition is a fundamental mathematical operation with widespread applications in various scientific, engineering, and everyday contexts. Here are several reasons why vector addition is important:

Representation of Physical Quantities:

Vectors are used to represent physical quantities that have both magnitude and direction, such as force, velocity, acceleration, and displacement. Vector addition allows us to combine these quantities accurately.

Force and Motion Analysis:

In physics, forces acting on an object are often represented as vectors. Vector addition enables the calculation of the net force acting on an object, providing insights into its motion and behaviour.

Projectile Motion:

Vector addition is crucial for understanding projectile motion. By breaking down the initial velocity vector into horizontal and vertical components, analysts can study the trajectory, range, and height of a projectile.

CBSE Class 11th Downloadable Resources: 

Being in CBSE class 11th and considering the board examinations you must be needing resources to excel in your examinations. At TestprepKart we take great pride in providing CBSE class 11th all study resources in downloadable form for you to keep you going. 

Below is the list of all CBSE class 11th Downloads available on TestprepKart for both Indian and NRI students preparing for CBSE class 11th in UAE, Oman, Qatar, Kuwait & Bahrain. 

SAMPLE PRACTICE QUESTIONS OF SIGNIFICANT FIGURES :

Q1. What is Vector Addition?

Answer: Vector addition is the process of combining two or more vectors to find their resultant or sum. It involves both magnitude and direction.

Q2. What is the Analytical Method of Vector Addition?

Answer: The analytical method involves breaking down vectors into their components along specified axes (usually x and y), adding the corresponding components separately, and then reconstructing the resultant vector from the sum of the components.

Q3. How are Vectors Represented Analytically?

Answer: Vectors are represented analytically by expressing their components along a chosen set of coordinate axes. For example, a vector A can be represented as ^A=Ax​i^+Ay​j^​, where Ax​ and  Ay​ are the vector components along the x and y axes, respectively.

Q4. What is the Resultant Vector in Analytical Vector Addition?

Answer: The resultant vector is the vector sum obtained by adding the corresponding components of the individual vectors. It is represented as ^R=Rx​i^+Ry​j^​, where Rx​ and Ry​ are the resultant vector components along the x and y axes.

Q5. How is Magnitude Determined in Analytical Vector Addition?

Answer: The magnitude of the resultant vector is determined using the Pythagorean theorem: 2R=Rx2​+Ry2​​.

Download Question Bank