Triangles, the fundamental shapes that form the backbone of geometry, are a captivating realm within the world of mathematics. In this blog post, we embark on a fascinating journey into the intricate world of triangles, unraveling their properties, classifications, and the profound role they play in various mathematical and real-world scenarios.

Triangles Unleashed Navigating the Geometric Wonders and Applications of Triangular Marvels

What Is a Triangle?

A triangle can be defined as a polygon that has three angles and three sides. The interior angles of a triangle sum up to 180 degrees, and the exterior angles sum up to 360 degrees.

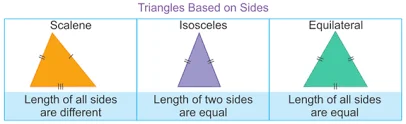
Scalene Triangle – All three sides of the triangle are of different measure

Isosceles Triangle – Any two sides of the triangle are of equal length

Equilateral Triangle – All three sides of a triangle are equal and each angle measures 60 degrees

Acute angled Triangle – All the angles are smaller than 90 degrees

Right angle Triangle – Any of the three angles is equal to 90 degrees

Obtuse-angled Triangle – One of the angles is greater than 90 degrees

Download Mathematics notes

The Basics

Triangles are polygons with three sides and three angles, but their simplicity belies their complexity. Understanding the basics of angles, sides, and vertices sets the stage for delving deeper into the rich tapestry of triangle properties.

Classifications

Triangles come in diverse forms, each with its unique set of characteristics. From equilateral triangles, where all sides and angles are equal, to isosceles and scalene triangles, each classification opens a door to a new realm of geometric possibilities.

Properties

Exploring the interior and exterior angles, the Pythagorean theorem, and the Law of Sines and Cosines reveals the hidden symmetries and relationships within triangles. These properties not only form the foundation of geometry but also find practical applications in fields ranging from architecture to physics.

Applications

Triangles have a ubiquitous presence in our surroundings. From the stability of architectural structures to the calculations involved in navigation, triangles play a vital role in diverse fields. Unraveling these applications showcases the real-world significance of this geometric wonder.

Challenges and Puzzles

Engaging with triangles often involves solving puzzles and problems that stimulate critical thinking. From classic geometry problems to real-world conundrums, tackling these challenges not only sharpens mathematical skills but also fosters a deeper appreciation for the elegance of triangles.

Basic Proportionality Theorem

In Mathematics, the basic proportionality theorem states that “If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.”

Now, let us understand the Basic proportionality theorem with the help of a diagram.
Consider the triangle ABC, as depicted in the diagram. We draw a line PQ parallel to the side BC of ABC and intersect the sides AB and AC in P and Q, respectively.
Thus, according to the Basic proportionality theorem,
AP/PB = AQ/QC

To know more about the Basic Proportionality Theorem.

CBSE Class 10 NCERT Mathematics Topics for a Strong Foundation (NCERT DOWNLOAD)

Similarity Criteria of Triangles

Mathematical Expression for Similarity
In Δ ABC and Δ DEF, if
(i) ∠ A = ∠ D, ∠ B = ∠ E, ∠ C = ∠ F and
(ii)AB/DE = BC/ EF = CA/ FD, then the two triangles are similar.
To find whether the given two triangles are similar or not, it has four criteria. They are:

• Side-Side-Side (SSS) Similarity Criterion – When the corresponding sides of any two triangles are in the same ratio, then their corresponding angles will be equal, and the triangle will be considered similar triangles.

• Angle Angle Angle (AAA) Similarity Criterion – When the corresponding angles of any two triangles are equal, then their corresponding side will be in the same ratio, and the triangles are considered to be similar.

• Angle-Angle (AA) Similarity Criterion – When two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are considered similar.

• Side-Angle-Side (SAS) Similarity Criterion – When one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportional), then the triangles are said to be similar.

CBSE Class 10 Board Exam Sample Paper

Download Question Bank

[Previous Year Question Solution Maths Download Button] 
[Previous Year Question Solution Science Download Button]

CBSE Class 10th Downloadable Resources: 

Being in CBSE class 10th and considering the board examinations you must be needing resources to excel in your examinations. At TestprepKart we take great pride in providing CBSE class 10th all study resources in downloadable form for you to keep you going. 

Below is the list of all CBSE class 10th Downloads available on TestprepKart for both Indian and NRI students preparing for CBSE class 10th in UAE, Oman, Qatar, Kuwait & Bahrain. 

FAQ

Q1 What is a triangle?

Ans  A triangle is a polygon with three sides, three angles, and three vertices.

Q2  What are the different types of triangles?

Ans  Triangles can be classified into three types based on side lengths: equilateral (all sides equal), isosceles (two sides equal), and scalene (no sides equal).

Q3  What is the significance of the Pythagorean theorem in triangles?

Ans The Pythagorean theorem establishes a relationship between the sides of a right-angled triangle, stating that the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Q4  How are triangles used in architecture and construction?

Ans Triangles provide stability in architectural structures. Trusses, a framework of triangles, are commonly used to distribute weight and maintain structural integrity.

Q5 What are interior and exterior angles in a triangle?

Ans  Interior angles are the angles inside a triangle, while exterior angles are formed by extending one side of the triangle.